1. Quantum dynamics量子动力学
到目前为止,所有的势能函数均与时间无关:
$${V{(r,t)}} = {V{(r)}}$$
这种情况下,薛定谔方程可通过分离变量求解:
$$i\hbar \frac{{\partial \psi }}{{\partial t}} = H\psi $$ $$\Psi (r,t) = \psi (r){e^{ – iEt/\hbar }}$$
其中 ψ(r) 满足不含时薛定谔方程
时间相关性由指数因子(e-iEt/ћ)体现,但在构建 |Ψ|2时互相抵消,导致所有概率和期望值不随时间变化
将定态线性组合,可以使得波函数具有时间相关性,但测量能量的可能值及其出现概率依然是固定的
为了使一个能级可以跃迁到另一个能级,需要引入含时微扰项
当哈密顿量含时部分小于不含时部分,则可将其处理为微扰
2. Two-level systems二能级体系
假设未微扰体系中仅存在两个态, ψa 和 ψb,都是未微扰哈密顿量H0的本征态
$${H^0}{\psi _a} = {E_a}{\psi _a}$$ $${H^0}{\psi _b} = {E_b}{\psi _b}$$
这两个态正交归一
$$\langle{\psi_a}|{\psi _b}\rangle = {\delta_{ab}}$$
该体系内的任意态都可表示为这两个本征态的线性组合
$$\Psi (0) = {c_a}{\psi _a} + {c_b}{\psi _b}$$
$$\Psi (t) = {c_a}{\psi _a}{e^{ – i{E_a}t/\hbar }} + {c_b}{\psi _b}{e^{ – i{E_b}t/\hbar }}$$
$${\left| {{c_a}} \right|^2} + {\left| {{c_b}} \right|^2} = 1$$
3. The perturbed system
引入含时微扰H‘(t)
由于ψa 和 ψb 构成一个完备集,故可以通过线性组合表示 Ψ(t)
此时, ca 和 cb 是与时间有关的函数
$$\Psi (t) = {c_a}(t){\psi _a}{e^{ – i{E_a}t/\hbar }} + {c_b}(t){\psi _b}{e^{ – i{E_b}t/\hbar }}$$
问题归结为求解ca 和 cb随时间的变化规律
设粒子的初始状态为ψa(ca(0)=1, cb(0)=0), 经过时间t1,发现系数变为ca(t1)=0, cb(t1)=1, 这说明系统经历了从ψa 到 ψb的跃迁
Ψ(t)需满足含时薛定谔方程
$$\Psi (t) = {c_a}(t){\psi _a}{e^{ – i{E_a}t/\hbar }} + {c_b}(t){\psi _b}{e^{ – i{E_b}t/\hbar }}$$
$$i\hbar \frac{{\partial \psi }}{{\partial t}} = H\psi ,{\text{ }}H = {H^0} + H'(t)$$
$$i\hbar \frac{\partial }{{\partial t}}\left[ {{c_a}(t){\psi _a}{e^{ – i{E_a}t/\hbar }} + {c_b}(t){\psi _b}{e^{ – i{E_b}t/\hbar }}} \right]$$
$$\eqalign{
& i\hbar \left[ {{{\dot c}_a}{\psi _a}{e^{ – i{E_a}t/\hbar }} + {{\dot c}_b}{\psi _b}{e^{ – i{E_b}t/\hbar }} + {c_a}{\psi _a}\left( { – \frac{{i{E_a}}}{\hbar }} \right){e^{ – i{E_a}t/\hbar }} + {c_b}{\psi _b}\left( { – \frac{{i{E_b}}}{\hbar }} \right){e^{ – i{E_b}t/\hbar }}} \right] \cr
& = {c_a}[{H^{\text{0}}}{\psi _a}]{e^{ – i{E_a}t/\hbar }} + {c_b}[{H^{\text{0}}}{\psi _b}]{e^{ – i{E_b}t/\hbar }} + {c_a}[H'{\psi _a}]{e^{ – i{E_a}t/\hbar }} + {c_b}[H'{\psi _b}]{e^{ – i{E_b}t/\hbar }} \cr} $$
$$\left( {{H^0} + H'(t)} \right)\left( {{c_a}(t){\psi _a}{e^{ – i{E_a}t/\hbar }} + {c_b}(t){\psi _b}{e^{ – i{E_b}t/\hbar }}} \right)$$
考虑到$${H^0}{\psi _a} = {E_a}{\psi _a}$$ $${H^0}{\psi _b} = {E_b}{\psi _b}$$
上式左右两侧各有两项抵消
$${c_a}[H'{\psi _a}]{e^{ – i{E_a}t/\hbar }} + {c_b}[H'{\psi _b}]{e^{ – i{E_b}t/\hbar }} = i\hbar \left[ {{{\dot c}_a}{\psi _a}{e^{ – i{E_a}t/\hbar }} + {{\dot c}_b}{\psi _b}{e^{ – i{E_b}t/\hbar }}} \right]$$
为了分离${\dot c_a}$, 左右两侧与ψa做内积,并利用ψa和 ψb的正交性
$${c_a}\langle {\psi _a}|H’|{\psi _a}\rangle {e^{ – i{E_a}t/\hbar }} + {c_b}\langle {\psi _a}|H’|{\psi _b}\rangle {e^{ – i{E_b}t/\hbar }} = i\hbar {\dot c_a}{e^{ – i{E_a}t/\hbar }}$$
简单起见,定义
$$H’_{{ij}} \equiv \langle {\psi _i}|H’|{\psi _j}\rangle $$
$$H’_{{{\text{j}}i}} = {(H’_{{ij}})^*}$$
$${\dot c_a} = – \frac{i}{\hbar }\left[ {{c_a}H’_{{aa}} + {c_b}H’_{{ab}}{e^{ – i({E_b} – {E_a})t/\hbar }}} \right]$$
类似地, 与ψb做内积能够得到${\dot c_b}$
$${c_a}\langle {\psi _b}|H’|{\psi _a}\rangle {e^{ – i{E_a}t/\hbar }} + {c_b}\langle {\psi _b}|H’|{\psi _b}\rangle {e^{ – i{E_b}t/\hbar }} = i\hbar {\dot c_b}{e^{ – i{E_b}t/\hbar }}$$
$${\dot c_b} = – \frac{i}{\hbar }\left[ {{c_b}H’_{{bb}} + {c_a}H’_{{ba}}{e^{i({E_b} – {E_a})t/\hbar }}} \right]$$
一般地, H‘ 的对角元为0
$$H’_{{aa}} = H’_{{bb}} = 0$$
$${\dot c_a} = – \frac{i}{\hbar }H’_{{ab}}{e^{ – i{\omega _0}t}}{c_b},{\text{ }}{\dot c_b} = – \frac{i}{\hbar }H’_{{ba}}{e^{i{\omega _0}t}}{c_a}$$
其中 ${\omega _0} \equiv \frac{{{E_b} – {E_a}}}{\hbar }$ (假设Eb≥Ea, 故 ω0 ≥0)
4. Time-dependent perturbation theory 含时微扰理论
到目前为止,并没有限定微扰的尺度
但如果H‘ 是小量, 则可用连续近似地方法处理
假设初始时刻粒子处于低能态
$${c_a}(0) = 1,{\text{ }}{c_b}(0) = 0$$
如果没有扰动,则粒子永远处于这个态 (为什么?)
Zeroth Order
$${c_a}^{(0)}(t) = 1,{\text{ }}{c_b}^{(0)}(t) = 0$$
计算一级近似,将零级近似的值代入下式右侧
H’是小量
$${\dot c_a} = – \frac{i}{\hbar }H’_{{ab}}{e^{ – i{\omega _0}t}}{c_b},{\text{ }}{\dot c_b} = – \frac{i}{\hbar }H’_{{ba}}{e^{i{\omega _0}t}}{c_a}$$
First Order
$$\frac{{dc_a^{(1)}}}{{dt}} = 0 \Rightarrow c_a^{(1)}(t) = 1$$
此处的上标含义与前面不同,是“整体”而非“差值”
$$\frac{{dc_b^{(1)}}}{{dt}} = – \frac{i}{\hbar }H’_{{ba}}{e^{i{\omega _0}t}} \Rightarrow c_b^{(1)} = – \frac{i}{\hbar }\int_0^t {H’_{{ba}}(t’){e^{i{\omega _0}t’}}} dt’$$
同理,计算二级近似,将一级近似的值代入右侧
Second Order
$$\dot c_a^{(2)} = – \frac{i}{\hbar }H’_{{ab}}{e^{ – i{\omega _0}t}}c_b^{(1)}$$
$$c_b^{(1)} = – \frac{i}{\hbar }\int_0^t {H'{_{ba}}(t’){e^{i{\omega _0}t’}}} dt’$$
$$\eqalign{
& \frac{{dc_a^{(2)}}}{{dt}} = – \frac{i}{\hbar }H’_{{ab}}{e^{ – i{\omega _0}t}}\left( { – \frac{i}{\hbar }} \right)\int_0^t {H’_{{ba}}(t’){e^{i{\omega 0}t’}}} dt’ \Rightarrow \cr & c_a^{(2)}(t) = 1 – \frac{1}{{{\hbar ^2}}}\int_0^t {H’_{{ab}}(t’){e^{ – i{\omega 0}t’}}} \left[ {\int_0^{t’} {H’_{{ba}}(t^”){e^{i{\omega _0}t^”}}} dt^”} \right]dt’ \cr} $$
$${\text{ }}\dot c_b^{(2)} = – \frac{i}{\hbar }H'{_{ba}}{e^{i{\omega _0}t}}c_a^{(1)}$$
$$c_a^{(1)}(t) = 1$$
$$c_b^{({\text{2}})} = – \frac{i}{\hbar }\int_0^t {H'{_{ba}}(t’){e^{i{\omega _0}t’}}} dt’$$
cb 不变, $c_b^{({\text{2}})}({\text{t}}) = c_b^{({\text{1}})}({\text{t}})$
ca(2) (t) 的表达式中包含零级项,因此二级修正项仅是积分部分
上述步骤可一直重复下去:将第n级近似插入右侧,解出第n+1级近似
$${c_a}^{(0)}(t) = 1,{\text{ }}{c_b}^{(0)}(t) = 0$$
$$c_a^{(1)}(t) = 1,c_b^{(1)} = – \frac{i}{\hbar }\int_0^t {H'{_{ba}}(t’){e^{i{\omega _0}t’}}} dt’$$
$$\eqalign{
& c_a^{(2)}(t) = 1 – \frac{1}{{{\hbar ^2}}}\int_0^t {H’_{{ab}}(t’){e^{ – i{\omega _0}t’}}} \left[ {\int_0^{t’} {H’_{{ba}}(t^”){e^{i{\omega 0}t”}}} dt^”} \right]dt’ \cr & c_b^{({\text{2}})} = – \frac{i}{\hbar }\int_0^t {H’_{{ba}}(t’){e^{i{\omega _0}t’}}} dt’ \cr} $$
零级项不含H‘, 一级项含有一个H‘, 二级项含有两个H‘, 依此类推
一级近似的误差可从下式看出:
$${\left| {c_a^{(1)}(t)} \right|^2} + {\left| {c_b^{(1)}(t)} \right|^2} \ne 1$$
然而,如果仅考虑到H’的一级项,
$${\left| {c_a^{(1)}(t)} \right|^2} + {\left| {c_b^{(1)}(t)} \right|^2} = 1$$
同理适用于高级项
5. Sinusoidal Perturbations正弦扰动
假设微扰与时间存在正弦关系:
$$H’_(r,t) = V(r)\cos (\omega t)$$
$$H’_{{ab}} = {V_{ab}}\cos (\omega t)$$
其中$${V_{ab}} \equiv \langle {\psi _a}|V|{\psi _b}\rangle $$
一级近似下,有
$$c_b^{(1)} = – \frac{i}{\hbar }\int_0^t {H'{_{ba}}(t’){e^{i{\omega _0}t’}}} dt’$$
将H‘ab代入上式
$$\eqalign{
& {c_b} \cong – \frac{i}{\hbar }{V_{ba}}\int_0^t {\cos (\omega t’){e^{i{\omega 0}t’}}} dt’ = – \frac{{i{V_{ba}}}}{{2\hbar }}\int_0^t {\left[ {{e^{i({\omega 0} + \omega )t’}} + {e^{i({\omega _0} – \omega )t’}}} \right]} dt’ \cr & {\text{ }} = – \frac{{{V_{ba}}}}{{2\hbar }}\left[ {\frac{{{e^{i({\omega _0} + \omega )t}} – 1}}{{{\omega _0} + \omega }} + \frac{{{e^{i({\omega _0} – \omega )t}} – 1}}{{{\omega _0} – \omega }}} \right] \cr} $$
假设驱动频率(driving frequencies, ω) 与跃迁频率(transition frequency ω0), 非常接近,则上式中第二项占主导;即
$${\omega _0} + \omega \gg \left| {{\omega _0} – \omega } \right|$$
上式不全是限制,因为其他频率的微扰一般很难造成跃迁
下面将该理论应用于光,其频率ω~1015 s-1, 因此两项的分母都非常大,除非在ω0 附近
忽略第一项,得到
$$\eqalign{
& {c_b}(t) \cong – \frac{{{V_{ba}}}}{{2\hbar }}\frac{{{e^{i({\omega 0} – \omega )t/2}}}}{{{\omega _0} – \omega }}\left[ {{e^{i({\omega _0} – \omega )t/2}} – {e^{ – i({\omega _0} – \omega )t/2}}} \right] \cr & {\text{ }} = – i\frac{{{V_{ba}}}}{\hbar }\frac{{\sin [({\omega _0} – \omega )t/2]}}{{{\omega _0} – \omega }}{e^{i({\omega _0} – \omega )t/2}} \cr} $$
跃迁概率(transition probability):初态为ψa的粒子在t时刻时处于态 ψb的概率
$${P_{a \to b}}(t) = {\left| {{c_b}(t)} \right|^2} \cong \frac{{{{\left| {{V_{ba}}} \right|}^2}}}{{{\hbar ^2}}}\frac{{{{\sin }^2}[({\omega _0} – \omega )t/2]}}{{{{({\omega _0} – \omega )}^2}}}$$
跃迁概率也随时间正弦振荡
跃迁概率升高至最大值|Vab|2/ћ2(ω0 – ω)2后,重新降为0。但该最大值应远小于1,否则微扰不适用
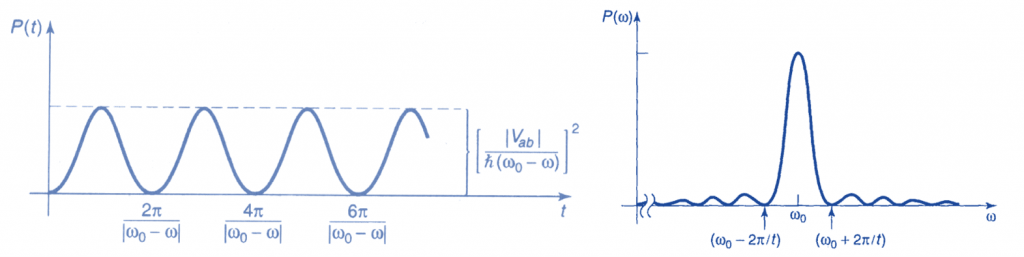
在时刻tn = 2nπ/|ω0 – ω|, n = 1, 2, 3, … , 粒子重新处于基态
当驱动频率与固有频率ω0接近时,跃迁概率接近于最大值,高度为 (|Vab|t/2ћ)2 ,宽度为4π / t
随时间延长,峰值越高越宽,但接近于1时微扰不再适用,故仅适用于较短t

