1. 定态微扰论
1.1 简介
量子力学中研究保守物理体系(即)哈密顿算符不明显地依赖于时间的体系)是以哈密顿算符的本征值方程为基础的。
两个重要例子:
简谐振子 特点:√ 哈密顿算符非常简单
氢原子 特点:√ 本征方程可精确求解
然而,仅有少数体系可精确求解。
一般情况下,方程过于复杂,无法求得解析解。
例如:无法精确求解多电子原子体系,哪怕是仅多了一个电子的氦原子。
近似方法:解析地求得基本的本征值方程的近似解
定态微扰论:应用极其广泛,很符合物理学家的口味
①首先突出主要的效应,也就是决定该现象或该体系全貌的那些效应
②理解了这些问题之后,再考虑在一级近似中忽略了的次要效应,并尝试着去解释更“精细”的细节
③正是在处理这些次要效应时,需要应用微扰理论。
1.2 Nondegenerate perturbation theory
非简并微扰:
微扰论适用的前提条件
①体系的哈密顿量H 可写成如下形式:
$$H = {H_0} + W$$
其中H0 的本征态和本征值已知,W远小于H0算符怎么比大小?
②实际上指的是W的矩阵元要远小于H0;
③H0与时间无关,称为非微扰哈密顿量(unperturbed Hamiltonian),而W称为微扰;
④如果W也与时间无关,则称为定态微扰;
⑤求解微扰造成的能级和波函数变化。
基本假设与方法
假设W正比于一个实数λ,其无量纲且远小于1。
$$W = \lambda \hat W$$
$$\lambda \ 1$$
算符 W ̂ 的矩阵元与H0可比(comparable)
一句话弄懂微扰理论:
将H的本征值和本征态按λ幂次展开,保留有限项。
具体步骤
①假设未微扰哈密顿量H0 的本征态与本征值已知;
②假设上述本征值构成分立谱(discrete spectrum),并可以用一个整数序号p代表:Ep0;
③对应的本征态可表示为 |$\varphi _p^i$〉,多余的序号i用于简并态Ep0,区分本征子空间中的正交归一基矢。
$${H_0}|\varphi _p^i\rangle = E_p^0|\varphi _p^i\rangle $$
$$\langle \varphi p^i|\varphi {p’}^{i’}\rangle = {\delta {pp’}}{\delta {ii’}},\sum\limits_p {\sum\limits_i {|\varphi _p^{\mathop i\limits^. }\rangle \langle \varphi _p^{\mathop i\limits^. }| = I} } $$
微扰强度λ
$$H(\lambda ) = {H_0} + \lambda \hat W$$
① 体系的哈密顿量可看作λ 的函数,而λ 则表征微扰的强度大小;
② λ 等于0,H(λ) 等于未微扰的哈密顿量H0;
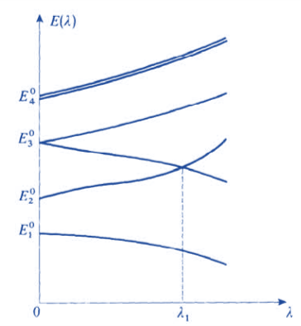
③ H(λ) 的本征值E(λ) 一般情况下与λ有关;
④ 每条曲线都对应着H(λ)的一个本征矢;
⑤ 每一个λ对应的若干本征矢构成矢量空间的一组基矢;
⑥ H(λ) 可以存在简并;
⑦ 当λ→0时,不同E(λ)可以趋近同一个未微扰本征值 Ep0。
1.3 H(λ) 本征方程的近似解
问题描述:
① 寻找H(λ)的本征态 |ψ(λ)〉和本征值E(λ)
$$H(\lambda )|\psi (\lambda )\rangle = E(\lambda )|\psi (\lambda )\rangle $$
②假设E(λ)和|ψ(λ)>可按λ幂次展开:
$$E(\lambda ) = {\varepsilon _0} + \lambda {\varepsilon _1} + … + {\lambda ^q}{\varepsilon _q} + …$$
$$|\psi (\lambda )\rangle = |0\rangle + \lambda |1\rangle + … + {\lambda ^q}|q\rangle + …$$
注意这个写法,与前面右矢的标记不同。
③ 替换 $({H_0} + \lambda \hat W)\left[ {\sum\limits_{q = 0}^\infty {{\lambda ^q}} |q\rangle } \right] = [\sum\limits_{q’ = 0}^\infty {{\lambda ^{q’}}} {\varepsilon {q’}}]\left[ {\sum\limits{q = 0}^\infty {{\lambda ^q}} |q\rangle } \right]$
④ λ取任意值(小),等式两侧都应成立;
⑤ 为此要求两侧相同λ幂次的系数相等
$$({H_0} + \lambda \hat W)\left[ {\sum\limits_{q = 0}^\infty {{\lambda ^q}} |q\rangle } \right] = [\sum\limits_{q’ = 0}^\infty {{\lambda ^{q’}}} {\varepsilon {q’}}]\left[ {\sum\limits{q = 0}^\infty {{\lambda ^q}} |q\rangle } \right]$$
· For 0th-order terms in λ
$${H_0}|0\rangle = {\varepsilon _0}|0\rangle $$
· For 1st-order terms in λ
$$({H_0} – {\varepsilon _0})|1\rangle + (\hat W – {\varepsilon _1})|0\rangle = 0$$
· For 2nd-order terms in λ
$$({H_0} – {\varepsilon _0})|2\rangle + (\hat W – {\varepsilon _1})|1\rangle – {\varepsilon _2}|0\rangle = 0$$
· For qth-order terms in λ
$$({H_0} – {\varepsilon _0})|q\rangle + (\hat W – {\varepsilon _1})|q – 1\rangle – {\varepsilon _2}|q – 2\rangle \; – {\varepsilon _q}|0\rangle = 0$$
只关注前三个等式,即忽略λ2以上的项
前面学过,本征方程
$$H(\lambda )|\psi (\lambda )\rangle = E(\lambda )|\psi (\lambda )\rangle $$
所确定的 |ψ(λ)> 可与任意系数相乘。
因此,可按以下规则选取|ψ(λ)> 的模和相角(相位因子)
· |ψ(λ)>归一化;
· 调整相角,使得内积<0|ψ(λ)> 为实数。
对于0级小,这意味着用 |0> 表示的矢量是归一化的
$$\langle 0|0\rangle = 1$$
此时相角任意选择
对于1级小,矢量|ψ(λ)>模的平方可写为:
$$\langle \psi (\lambda )|\psi (\lambda )\rangle = [\langle 0| + \lambda \;\langle \;1|][|0\rangle + \lambda |1\rangle ] + O({\lambda ^2})$$
$$ = \;\langle \;0|0\rangle + \lambda [\langle 1|0\rangle + \langle 0|1\rangle ] + O({\lambda ^2})$$
要令上式等于1,则 λ的一次项应等于0
选择相角,使<0|1>为实数(λ为实数),则可以得到
$$\langle 0|1\rangle = \langle 1|0\rangle = 0$$
注意这是一个人为选择的结果
类似地,讨论λ的二级小,可以得到
$$\langle 0|2\rangle = \langle 2|0\rangle = – \frac{1}{2}\langle 1|1\rangle $$
推广到q级小,则有
$$\eqalign{
& \langle 0|q\rangle = \langle q|0\rangle = – \frac{1}{2}[\langle q – {\text{1}}|1\rangle + \langle q – 2|2\rangle + … \cr
& {\text{ }} + \langle 2|q – 2\rangle + \langle 1|q – 1\rangle ] \cr} $$
1.4 The perturbation subspace
微扰子空间
$${H_0}|0\rangle = {\varepsilon _0}|0\rangle $$
上式说明,|0>是 H0 具有本征值 ε0的本征矢;
ε0属于H0 的能量谱,因为H(λ)的每一个本征值,当λ→0时都会趋近于其中一个未微扰的能级;
不妨令ε0 = E0,则当λ→0时,会有一个或多个不同的E(λ) 趋近于En0;
考虑这些属于上述E(λ)的本征态;
这些本征矢张开一个子空间,当λ在0附近变化时,其维度不能突变
最终,子空间的维度等于En0的简并度 gn
特别地,如果En0是非简并,则仅能对应一个本征值E(λ), 且该能级是非简并的
一直到这里,并未区分能级简并与否
1.5 Perturbation of a non-degenerate level
非简并能级的微扰: 注意:微扰的对象是能级,而非体系
· 考虑未微扰哈密顿量H0的非简并能级En0,其本征态为|φn> 注意这个符号,小写的。
· 目标:微扰W作用后能级和定态波函数的变化;
· 对于H(λ)当λ→0时趋近于En0 的本征值,存在关系:
$${\varepsilon _0} = E_n^0$$
· 这表明|0> 正比于|φn>。
· p|0>和|φn>都是归一化的,因此选择
$$|0\rangle = |{\varphi _n}\rangle $$
这样,当 λ→0时,就又得到了具有相同相角的未微扰态 |φn>
H(λ)的本征值En(λ) ,当 λ→0时趋近于H0的本征值En0
假设λ 足够小,这样本征值仍然是非简并的,即只对应于一个特定的 |ψn(λ)>。
1.6 First-order corrections一级修正
p先确定ε1 和|1>
Energy correction能量修正
$$({H_0} – {\varepsilon _0})|1\rangle + (\hat W – {\varepsilon _1})|0\rangle = 0$$
将上式投影至|φn>, 可得
$$\langle {\varphi _n}|({H_0} – {\varepsilon _0})|1\rangle + \langle {\varphi _n}|(\hat W – {\varepsilon _1})|0\rangle = 0$$
第一项等于0,因为|φn>=|0> 是H0的本征态,其本征值为 En0=ε0
$${\varepsilon _1} = \langle {\varphi _n}|\hat W|0\rangle = \langle {\varphi _n}|\hat W|{\varphi _n}\rangle $$
$${\varepsilon _1} = \langle {\varphi _n}|\hat W|0\rangle = \langle {\varphi _n}|\hat W|{\varphi _n}\rangle $$
在非简并态的情况下,对应于En0 的 H 的本征值En(λ) 在微扰的一级修正下可写为
$${E_n}(\lambda ) = E_n^0 + \langle {\varphi _n}|W|{\varphi _n}\rangle + O({\lambda ^2})$$
$W = \lambda \hat W$ 注意两个W的区别
因此,能量的一级修正,等于微扰项在未微扰态|φn>中的平均值










